◼︎ 통계 기본 용어
모집단(Population) : 통계분석 방법을 적용할 관심 대상의 전체 집합
모수(Parameters) : 모집단을 분석하여 얻어지는 결과 수치
표본(Sample) : 직접적인 조사 대상이 된 모집단의 일부
통계량(Statistics) : 표본을 분석하여 얻어지는 결과 수치
◼︎ (기술)통계량 의 종류
1-1) 평균(Mean)
분산의 계산, 모수 추정, 가설 검증 등 통계 분석의 대표적인 값으로 널리 사용됨
극단적인 값(이상치)에 민감하여, 자료의 수가 적고 극단 값이 여러 개인 경우 대푯값의 기능을 상실
1-2) 기대값 E(X)
평균이 수치형 데이터에 대한 대표값이라면, 기대값은 모르는 데이터에 대한 평균값이라 할 수 있음
2) 중앙값(Median) = 중위수
데이터를 순서대로 나열할 때 가운데 있는 값
짝수일 경우, 양옆의 수를 더한 후, 2로 나눔
이상치에 민감하지 않기 대문에 극단적인 이상치가 있는 경우, 평균 대신 대푯값으로 사용될 수 있음
3) 최빈값(Mode)
데이터 중에서 빈도가 가장 많은 값
자료에 따라 존재하지 않을 수 있고 유일한 값이 아닐 수도 있음
질적 변수에도 활용 가능, 즉, 명목, 서열자료에서 대푯값으로 사용
열 = 변수(Variable) = Feature(특성) = Attribute(속성)
행 = Observation = instance
값 = Label = class = target
◼︎ 변이 통계량 (산포도 = 분산도)
: 자료가 흩어져 있는 정도(퍼진 정도)를 측정
두 분포에서 자료의 흩어짐을 비교하는 데 이용
1) 최솟값(Minimum)
2) 최댓값(Maximum)
3) 범위(Range) : 최소값과 최대값의 차이
4) 분산(Variance)
모든 편차를 제곱하고 이를 합한 후 자료 개수로 나눈 값
표본표준편차를 구할 경우 (자료 개수 - 1) 로 나눔
두 분포에서 자료의 흩어짐을 비교하는 데 이용
원 자료의 단위와 달라짐
5) 표준편차(Standard Deviation)
분산의 제곱근 (루트분산)
원래 자료의 단위로 환원되어 같은 단위로 측정된 평균이나 다른 통계량과 쉽게 비교할 수 있음
6) 변동계수(Coefficient of variation, CV) = 상대표준편차
표준편차를 평균으로 나눈 값
서로 다른 데이터 간의 편차를 비교하는 방법
- 모 변동계수(모집단에서), 표본변동계수(표본에서)
7) 백분위수(Percentile)
자료를 크기 순으로 정리하여 100등분 하였을 때 각 등분점에 위치하는 자료
50 백분위수는 중앙값과 같음
8) 사분위수(Quartile)
자료를 크기 순으로 정리하여 4등분 하였을 때 각 등분점에 위치하는 자료
Q1 = 1사분위수 = 25백분위수
Q2 = 2사분위수 = 50백분위수 = 중앙값
Q3 = 3사분위수 = 75백분위수
9) 사분위수범위(Inter Quartile Range, IQR)
1사분위수와 3사분위수의 차이
* 자유도
전체 데이터 중 실질적으로 독립적인 데이터들의 개수
자유도 = 자료 개수 -1 (일반적으로)
자유도를 고려하지 않은 표준편차는 실제 값을 과소 평가할 가능성이 높음
◼︎ 상자수염그림(Box plot)
자료분포의 특성을 그래프로 요약하는 방법
최소값, 1사분위수, 2사분위수(중앙값), 3사분위수, 최대값을 표현
◼︎ 위치 통계량 (분포의 모양)
: 데이터분포의 형태와 대칭성을 설명
1) 왜도(skewness) : 분포의 대칭성을 알아보는 측도 // 기울어진 정도(양수 오른쪽 꼬리)
2) 첨도(kurtosis) : 정규분포 대비 봉오리의 높이를 알아보는 측도 // 뽀족한 정도(양수 : 정규분포보다 뾰족)
◼︎ 자료유형
| 측정수준 | 범주특성 | |||||
| 상호배타성 포괄성 분류 (등가성) |
서열비교 | 표준측정단위 덧셈뺄셈 (간격일정) |
자연적 0 존재 곱셈나눗셈 (절대0) |
측정예시 | ||
| 질적 자료 |
명목척도 | 0 | X | X | X | 남녀, 정당이름 |
| 서열척도 | 0 | 0 | X | X | 직급(1급,2급), 상중하, 만족보통불만족 | |
| 양적 자료 |
등간척도 | 0 | 0 | 0 | X | 온도, 직무 만족도(1~5), IQ, 물가지수 |
| 비율척도 | 0 | 0 | 0 | 0 | 인구증가율, 가구당 소득, 재정자립도 | |
◼︎ 데이터 타입 별 분석 방법 및 시각화
- 데이터 타입
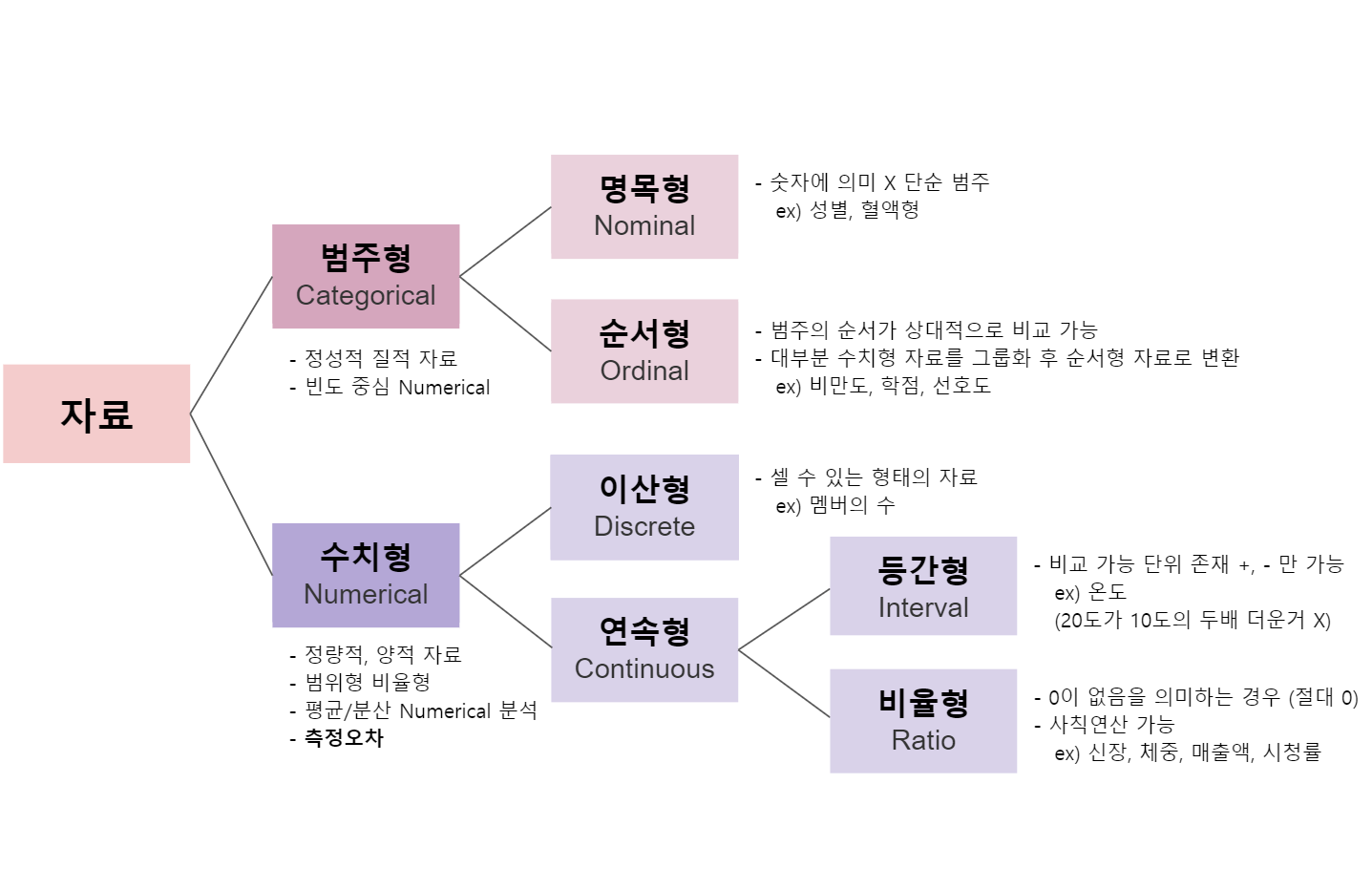
- 데이터 타입 별 시각화 방법
| 기초통계 | 시각화 | |
| 수치형(Numerical data) : 양적 데이터, 숫자 |
분포분석 - 데이터의 특성을 분포로 설명 - 주요 항목은 범위, 평균, 분산, 표준편차, 측정오차 등 - 대부분의 분석 방법이 특정 분포를 가정 |
히스토그램, box plot, 산점도 |
| 범주형(Categorical data) : 질적 데이터, 글자 |
빈도분석 - 범주별 출현 빈도에 기반한 분석 - 주요 항목은 빈도 , 비율, 누적비율등 - 특정 분포 가정없이 빈도에 기반한 확률을 사용 |
분할표, 파이그래프, 모자이크 plot |
- 데이터 타입 별 분석 방법
| 독립변수 X | |||
| 수치형 | 범주형 | ||
| 종속변수 Y | 수치형 | 상관분석 회귀분석 | t-test ANOVA |
| 범주형 | 로지스틱 회귀분석 | 카이제곱 검정 | |