◼︎ 확률변수와 확률분포
1) 확률변수
: 표본공간의 원소를 실수로 대응한 값
2) 확률분포
: 확률변수와 그 값이 나올 수 있는 확률을 대응시켜 표시하는 것
어떤 확률변수가 어떤 확률분포에 대응할 때, "확률분포에 따른다"라고 표현
ex) 동전던지기에서 HH을 0/ HT, TH를 1/ TT를 2로 맵핑
| 확률변수 | 0 | 1 | 2 |
| 확률분포 | 1/4 | 2/4 | 1/4 |
*범주형 데이터를 계산하기 위해 실수로 표현
◼︎ 확률분포함수
: 확률변수 X가 취할 확률을 X의 함수로 나타낸 것
1) 확률질량함수(probability mass function, PMF)
: 이산확률변수에서 특정한 값에 대한 확율을 나타내는 함수, 이산확률분포

특정한 위치에서 확률을 구할 수 있음
2) 확률밀도함수(probability density function, PDF)
: 연속확률변수에서 특정한 값에 대한 확률을 나타내는 함수, 연속확률분포

구간면적이 확률이됨
전체 면적 = 1, 대표적으로 정규분포가 있음
◼︎ 이산확률분포의 기대값과 분산
1)기대값의 특성
E(a) = a
E(bX) = bE(X)
E(a + bX) = a + bE(X)
E(X + Y) = E(X) + E(Y)
E(aX + Y) = aE(X) + bE(Y)
2)분산의 특성
Var(a) = 0
Var(a + x) = Var(x)
Var(bx) = b^2 Var(x)
Var(x + y) = Var(x) + Var(y) ( x, y독립일 때 )
Var(x + y) = Var(x) + Var(y) + 2Cov(x, y)
◼︎ 균등분포 (Uniform Distribution)
: 확률분포 함수가 정의된 모든 곳에서 값이 일정한 분포
(이산균등분포, 연속균등분포)

◼︎ 이항분포
베르누이실험 또는 베르누이 시행에 기초
*베르누이시행 : 결과가 딱 2가지만 나오는 것 (A인 케이스와 아닌 케이스)
이항분포, 포아송분포, 초기하분포가 이항분포에 해당
1) 조건
- 시행을 n번 반복
- 각 시행은 성공과 실패라는 상호 배타적인 결과를 갖음
- n번의 시행은 독립적
- 1번 새행할 때 성공확률 p와 실패확률 (1 - p)는 시행할 때마다 동일
- 확률변수 X는 n번 시행 중에서 성공횟수를 의미
2)특성
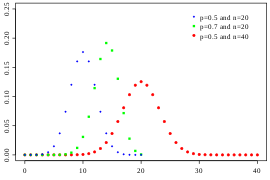
- 성공확률 p = 0.5에 가까우면 시행횟수 n의 크기에 관계없이 좌우대칭의 종모양
- 시행횟수n이 크면 성공확률 p의 크기에 상관없이 좌우대칭을 이룸
- 만일 p < 0.5이고 n이 작은 경우에 오른쪽 꼬리분포를 나타냄
- 만일 p > 0.5이고 n이 작은 경우에 왼쪽 꼬리분포를 나타냄
◼︎ 포아송분포 (Poisson Distribution)
1) 개념
: 일정한 단위시간, 단위거리, 단위면적과 같이 어떤 구간에서 어떤 사건이 랜덤하게 발생하는 경우에 사용할 수 있는 이산 형확률분포 (단위 시간에 일어날 횟수의 기대값이 람다라고 했을 때 그 사건이 k회 일어날 확률분포)

2)적용조건
- 구간마다 발생하는 사상은 서로 독립적이다.
- 사상의 발생확률은 구간의 길이에 비례한다.
- 아주 작은 구간에서 사상이 발생할 확률은 무시할만 하다.
- 구간마다 확률분포는 일정하다.
3)활용 예
1시간 동안 은행에 방문하는 고객의 수
1시간 동안 콜센터에 걸려오는 전화 수
책 한페이지 당 오탈자가 발생하는 건수
반도체웨이퍼 25장 당 불량 건수
*특정한 단위 안에서 발생되는 횟수의 값을 알아내고 싶을 때 사용하는 분포
포아송의 람다값이 커질 수록 정규분포에 수렴
(단위시간동안 사건발생 횟수(람다값) = 평균= 분산)
◼︎ 지수분포 (Exponential Distribution)
1) 개념
: 사건이 서로 독립일 때, 일정시간동안 발생하는 사건의 횟수가 포아송 분포를 따른다면, 다음 사건이 이러날 때 까지 대기시간 (단위 시간당 사건이 람다번 발생 기대, X만큼 기다릴 확률)
2)특징
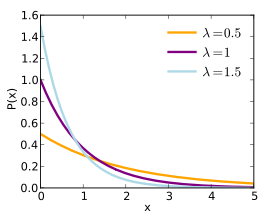
항상 양의 값만 가짐
시간이 지날 수록 확률 작아짐
평균은 람다의 역수, 분산은 평균 제곱
무기억성